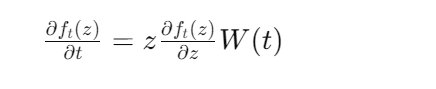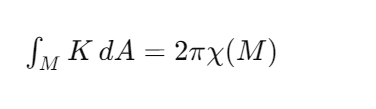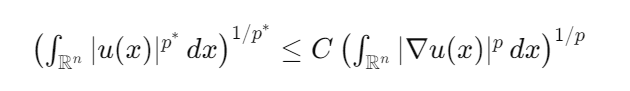Самые красивые уравнения по мнению математиков

Для многих математиков уравнения являются настоящими произведениями искусства. Как художественные шедевры или музыкальные композиции, математические выражения могут быть столь же увлекательными и вдохновляющими. Как и в искусстве, красота математики субъективна: одни предпочитают лаконичные уравнения, другие — более сложные и многослойные.

Вот некоторые из самых красивых математических уравнений, отобранные учеными, и причины, почему они считаются таковыми.

Уравнение Лёвенера

В 1923 году Чарльз Лёвнер представил уравнение, описывающее эволюцию семейства конформных функций, определённых на подмножествах комплексной плоскости.

Уравнение Лёвнера нашло применение в различных областях математики, включая теорию однолистных функций и геометрическую теорию функций. Однако его истинный потенциал раскрылся лишь спустя десятилетия.

В 1999 году израильско-американский математик Одед Шрамм сделал революционное открытие, объединив уравнение Лёвнера с теорией вероятностей. Шрамм обнаружил, что если в качестве управляющей функции ξ(t) использовать броуновское движение, то получающиеся решения обладают замечательными свойствами конформной инвариантности и масштабной инвариантности.

Это открытие привело к созданию теории стохастических процессов Лёвнера (SLE - Schramm-Loewner Evolution), которая предоставила мощный инструмент для изучения критических явлений в двумерных системах статистической механики. SLE позволила строго доказать многие гипотезы, долгое время остававшиеся недоступными для математического анализа.

Формула Гаусса-Бонне

Формула Гаусса-Бонне в дифференциальной геометрии устанавливает равенство между интегралом гауссовой кривизны по поверхности и произведением константы на характеристику Эйлера этой поверхности. Это уравнение удивительно тем, что связывает кривизну поверхности с её топологией, демонстрируя, что общая кривизна остаётся неизменной при деформации поверхности. Оно было впервые сформулировано Карлом Фридрихом Гауссом и Пьером Оссианом Бонне в первой половине XIX века и до сих пор остается одним из самых красивых уравнений в геометрии.

Значимость этой теоремы многогранна. Она наглядно демонстрирует, что интеграл локальной геометрической величины по всей поверхности равен топологическому инварианту, умноженному на константу. Это означает, что общая интегральная кривизна поверхности остается неизменной при любых непрерывных деформациях, не меняющих топологию. Такая связь между геометрией и топологией открывает широкие возможности для исследований и применений в различных областях математики и физики.

Теорема имеет важные обобщения, включая версии для поверхностей с краем и многомерные аналоги, такие как теорема Черна-Гаусса-Бонне для многообразий высших размерностей. Её приложения охватывают теорию Морса, теорию индекса эллиптических операторов и даже находят место в общей теории относительности.

Исторически, элементы этой теоремы были известны ещё Леонарду Эйлеру в контексте многогранников в XVIII веке. Карл Фридрих Гаусс доказал версию теоремы для геодезических треугольников в начале XIX века, а Пьер Оссиан Бонне обобщил результат на произвольные поверхности в 1848 году.

Теорема Гаусса-Бонне остаётся одним из самых элегантных и глубоких результатов в математике, демонстрируя удивительную гармонию между различными областями геометрии и топологии. Она продолжает вдохновлять математиков и физиков, открывая новые горизонты исследований и понимания структуры пространства.

Неравенство Соболева

Неравенства Соболева оценивают функции через их производные и лежат в основе понимания уравнений в частных производных. Особый интерес вызывает случай, когда неравенство не выполняется для n=2, что связано с уникальными свойствами этого измерения.

Эти неравенства играют ключевую роль в анализе регулярности решений таких уравнений и используются для доказательства существования и единственности решений.

Уравнение Римана-Роха

Уравнение Римана-Роха относится к комплексным римановым поверхностям и дивизорам на них. Оно имеет вид , где — это голоморфная характеристика Эйлера дивизора, — степень дивизора, а g — род поверхности. Это уравнение демонстрирует, что голоморфная характеристика Эйлера зависит только от топологических данных, раскрывая глубокие связи между топологией и комплексным анализом.

Теорема Римана-Роха демонстрирует, что эта характеристика, имеющая аналитическую природу, может быть выражена через чисто топологические данные (степень дивизора и род поверхности). Это раскрывает глубокую связь между комплексной структурой римановой поверхности и её топологией.

Значение теоремы выходит далеко за рамки теории римановых поверхностей. Она имеет обобщения на многомерные многообразия и играет ключевую роль в алгебраической геометрии, теории пучков и даже находит применения в теоретической физике.

Формула Эйлера

Формула Эйлера, также известная как произведение Эйлера, выражает глубокую связь между натуральными числами и простыми числами. Её элегантная запись скрывает удивительную мощь и универсальность. Эта формула не только предоставляет альтернативное доказательство бесконечности простых чисел, но и служит фундаментом для многих важных результатов в теории чисел.

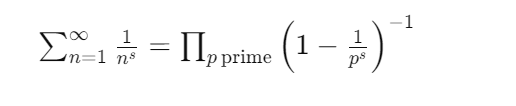
де p пробегает все простые числа, а n - все натуральные числа.

Значимость формулы Эйлера выходит далеко за рамки её первоначального применения. Она находит применение в аналитической теории чисел, криптографии и даже в некоторых областях физики. Современные математики продолжают использовать и расширять эту формулу, что свидетельствует о её непреходящей актуальности в математическом мире.

Уравнение (1/P) + (1/Q) + (1/R) = 1

Это уравнение имеет всего три решения в положительных целых числах: Его единственными решениями в натуральных числах являются p = q = r = 3; р = 2, q = г = 4; и p = 2, q = 3, r = 6. Оно связано с группами Коксетера и отображает границу между конечными и бесконечными группами отражений, а также с единственными способами замощения плоскости регулярными многоугольниками.

Эти уравнения не только красивы сами по себе, но и демонстрируют глубокие связи между различными областями математики, открывая новые пути для исследований и понимания.