Доказательство Бога: как Гедель заставил математику заговорить о вере

Кто бы мог подумать, что вопрос о существовании Бога может стать темой для эссе о математике? Не волнуйтесь, последующее обсуждение всё ещё твёрдо основано на научной основе. Однако вопрос о том, можно ли математически доказать существование Бога, весьма интригует. На самом деле, на протяжении веков несколько математиков неоднократно пытались доказать существование божественного существа. Среди них можно выделить Блеза Паскаля и Рене Декарта (в XVII веке), Готфрида Вильгельма Лейбница (в XVIII веке) и Курта Геделя (в XX веке), чьи работы по этой теме были опубликованы только в 1987 году. И, возможно, самое удивительное: в исследовании, впервые опубликованного в 2013 году, алгоритмический проверяющий подтвердил логическую цепочку Геделя — и нашел её абсолютно корректной. Неужели математика теперь окончательно опровергла утверждения всех атеистов?

Как можно догадаться, этого не произошло. Гедель действительно смог доказать, что существование чего-то, что он определил как божественное, необходимо вытекает из определённых предположений. Однако справедливость этих предположений вызывает сомнения. Например, если предположить, что все кошки трёхцветные, и зная, что трёхцветные кошки почти всегда женского пола, можно заключить: почти все кошки женского пола. Даже если логическое рассуждение верно, это, конечно, не соответствует действительности. Ведь само предположение о том, что все кошки трёхцветные, является ложным. Если делаются утверждения об окружающих нас вещах, таких как кошки, их можно проверить научными методами. Но когда речь идёт о доказательстве существования божественного существа, ситуация становится сложнее.

В то время как Лейбниц, Декарт и Гедель опирались на онтологическое доказательство Бога, выводя существование божественного существа из одной лишь возможности его существования с помощью логических умозаключений, Паскаль (1623–1662) выбрал несколько иной подход: он анализировал проблему с точки зрения того, что сегодня можно назвать теорией игр, и разработал так называемое "Пари Паскаля".

Для этого он рассмотрел два варианта: первый — Бог существует. Второй — Бога не существует. Затем он проанализировал последствия веры или неверия в Бога после смерти. Если существует божественное существо и человек верит в него, он попадёт в рай; иначе — отправится в ад. Если же Бога нет, то ничего не произойдёт — вне зависимости от того, был человек религиозен или нет. Лучшая стратегия, по мнению Паскаля, — это верить в Бога. В лучшем случае человек попадает в рай; в худшем случае — ничего не происходит. Если же не верить в Бога, то в худшем случае можно оказаться в аду.

Мысли Паскаля вполне понятны, но они касаются сценариев из религиозных текстов и не представляют собой доказательство существования высшего существа. Они лишь говорят о том, что верить в Бога стоит из чистого оппортунизма.

Онтологические подходы, связанные с природой бытия, кажутся более убедительными, даже если они, скорее всего, не изменят мнения атеистов. Теолог и философ Ансельм Кентерберийский (1033–1109) изложил свои идеи в начале прошлого тысячелетия. Он описал Бога как существо, больше которого нельзя вообразить ничего. Но если Бога не существует, то можно представить нечто большее: а именно, существо, больше которого ничего нельзя вообразить, но которое также существует и обладает свойством абсолютного величия. Это, конечно, абсурдно: ничто не может быть больше величайшего, что можно себе представить. Соответственно, предположение, что Бога не существует, должно быть неверным.

Потребовалось несколько столетий, чтобы эту идею вновь пересмотрели — и сделал это не кто иной, как Декарт (1596–1650). Предполагается, что он не знал о работах Ансельма, но предложил почти идентичный аргумент в пользу существования божественного совершенного существа. Лейбниц (1646–1716) занялся этой темой спустя несколько десятилетий и нашёл в ней изъян: по его мнению, Декарт не показал, что " совершенные свойства " определённых сущностей, начиная от треугольников и заканчивая Богом, совместимы. Лейбниц утверждал, что совершенство не может быть должным образом исследовано. Следовательно, невозможно опровергнуть, что совершенные свойства объединяются в одном существе. Таким образом, из возможности божественного существа следует его реальность. Так что, основываясь на аргументах Ансельма и Декарта, можно сделать вывод, что Бог существует. Однако с математической точки зрения эти мыслительные эксперименты стали по-настоящему серьёзными только благодаря усилиям Геделя . Это не слишком удивительно: учёный уже в 25 лет перевернул эту тему, показав, что математика всегда содержит истинные утверждения, которые невозможно доказать. Для этого он использовал логику. Именно эта логика позволила ему доказать существование Бога.

Гедель представил следующие аксиомы (Ax), теоремы (Th) и определения (Df):

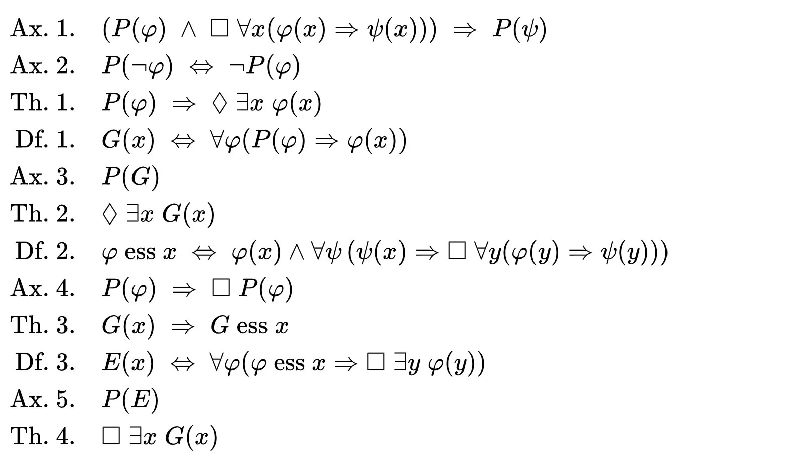
На первый взгляд они кажутся загадочными, но можно пройти их шаг за шагом, чтобы проследить ход мыслей Гёделя. Он начинает с аксиомы, то есть предположения: если у $\varphi$ есть свойство $P$, и из $\varphi$ всегда следует $\psi$, то $\psi$ также обладает свойством $P$. Для простоты можно предположить, что $P$ обозначает "положительное". Например, если фрукт вкусный — это положительное свойство, тогда его употребление в пищу приносит удовольствие. Следовательно, удовольствие от еды также является положительным свойством.

Вторая аксиома дополнительно устанавливает рамки для $P$. Если противоположность чего-то положительна, то это "что-то" должно быть отрицательным. Таким образом, Гедель разделяет мир на чёрное и белое: либо что-то хорошее, либо плохое. Например, если здоровье — это хорошо, то болезнь обязательно должна быть плохой.

С этими двумя посылками Гедель может вывести свою первую теорему: если $\varphi$ является положительным свойством, то существует вероятность того, что $x$ с таким свойством $\varphi$ существует. То есть, возможно существование положительных вещей.

Теперь математик впервые переходит к определению божественного существа: $x$ является божественным, если оно обладает всеми положительными свойствами $\varphi$. Вторая аксиома гарантирует, что Бог, определённый таким образом, не может иметь отрицательных характеристик (иначе возникло бы противоречие).

Третья аксиома гласит, что божественность — это положительная характеристика. Этот момент трудно оспорить, так как божественность объединяет все положительные характеристики.

Теперь вторая теорема становится немного более конкретной: комбинируя третью аксиому (божественность положительна) и первую теорему (возможно существование чего-то положительного), можно предположить, что может существовать божественное существо $x$.

Цель Геделя теперь состоит в том, чтобы показать на следующих шагах, что Бог должен существовать в рамках заданных предпосылок. Для этого он вводит во втором определении понятие "сущность" $\varphi$ объекта $x$, характерное свойство, которое определяет все остальные характеристики. Примером может служить "щенковость": если что-то обладает этим свойством, оно обязательно милое, пушистое и неуклюжее.

Четвёртая аксиома на первый взгляд не кажется слишком интересной. Она просто утверждает, что если что-то положительно, то оно всегда положительно — независимо от времени, ситуации или места. Быть "щенковым" и быть вкусным, например, всегда положительно, будь то днём или ночью, в Гейдельберге, Германия, или Буэнос-Айресе.

Теперь Гедель может сформулировать третью теорему: если существо $x$ является божественным, то божественность является его сущностным свойством. Это имеет смысл, так как если что-то является божественным, оно обладает всеми положительными характеристиками — и, следовательно, свойства $x$ фиксированы. Следующий шаг относится к существованию конкретного существа. Если где-то хотя бы одно существо $y$ обладает свойством $\varphi$, которое является сущностным свойством $x$, то $x$ также существует. Иными словами, если что-то обладает свойствами щенка, то щенки также должны существовать.

Согласно пятой аксиоме, существование является положительным свойством. Большинство людей согласится с этим.

Из этого можно заключить, что Бог существует, так как это существо обладает всеми положительными свойствами, а существование является положительным.

Как оказалось, логические выводы Геделя верны — даже компьютеры смогли это доказать. Тем не менее, эти выводы также подверглись критике. Помимо аксиом, которые, конечно, можно оспорить (почему мир должен делиться на «добро» и «зло»?), Гедель не даёт более подробной информации о том, что такое положительное свойство.

Это правда, что с помощью определений и аксиом можно описать множество $P$ математически:

• Если свойство принадлежит множеству, его отрицание не включается.
• Множество самодостаточно.
• Сущность множества имеет только характеристики множества и само является элементом множества.
• Множество всегда содержит одни и те же элементы — независимо от ситуации.
• Существование является частью множества.
• Если $\varphi$ является частью множества, то свойство иметь $\varphi$ в качестве сущности множества также включено в множество.

Однако всё это не гарантирует, что это множество уникально. Могут существовать несколько коллекций, удовлетворяющих требованиям. Например, как показали логики , можно построить случаи, когда, по определению Геделя, существует более 700 божественных сущностей, различающихся по сущности.

Этот факт не разрешает окончательный вопрос о существовании одного (или нескольких) божественных существ. Является ли математика действительно правильным способом ответа на этот вопрос, также остаётся под сомнением — хотя размышления об этом весьма захватывающи.