Три буквы, одна цифра, нож и каменный мост: как нарисованное уравнение изменило историю математики

16 октября 1843 года ирландский математик Уильям Роуэн Гамильтон совершил открытие, которое навсегда изменило мир математики. Во время прогулки вдоль Королевского канала в Дублине он внезапно осознал решение проблемы, над которой размышлял долгие месяцы. Вдохновлённый озарением, он вырезал уравнение на каменном мосту Брум, используя нож, который носил с собой. Уравнение выглядело так: «i² = j² = k² = ijk = –1». На первый взгляд оно может показаться простым, но его значение стало революционным для понимания математики и физики.

Гамильтон занимался задачей, связанной с описанием вращения объектов в трёхмерном пространстве. В тот период математики уже умели представлять положения объектов с помощью координат x, y и z. Однако, при повороте объекта вокруг оси требовались сложные расчёты, основанные на сферической геометрии, что делало задачу крайне трудоёмкой. Гамильтон стремился найти более простое и элегантное решение.

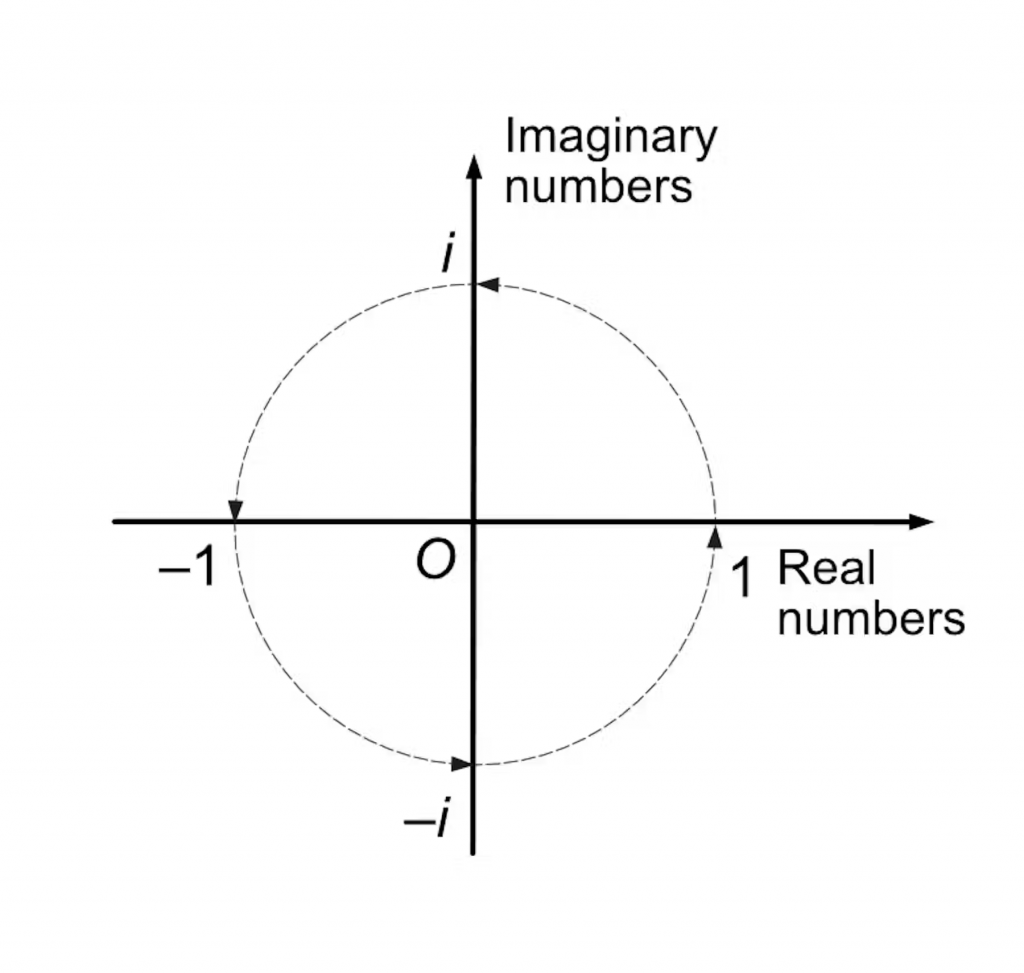
Вдохновение пришло из работы с комплексными числами, в которых реальная и мнимая части числа описывали двухмерные вращения. Мнимое число i, как известно, является квадратным корнем из –1 (i² = –1). Математики давно поняли, что умножение на i поворачивает объекты в плоскости на 90 градусов. Гамильтон задался вопросом, можно ли расширить эту концепцию на трёхмерное пространство.

Он много месяцев пытался найти способ описать трёхмерные вращения аналогично двумерным. В конце концов, ему пришла мысль, что для этого нужно добавить не только одно мнимое число, но и ещё два: j и k. При этом все три мнимых числа должны удовлетворять определённым условиям, которые он и выразил в своём уравнении на мосту: i² = j² = k² = ijk = –1. Это было его открытие кватернионов — четырёхмерных чисел, которые позволяли описывать вращения в трёхмерном пространстве.

Кватернионы оказались ключевым инструментом для вычисления вращений, что открыло двери для новых приложений в инженерии и физике. Особенно это стало полезным при разработке систем управления спутниками, роботами, а также в компьютерной графике, где вращения объектов в пространстве можно было рассчитывать гораздо проще и быстрее.

Однако настоящий прорыв произошёл, когда Гамильтон предложил разделять кватернионы на две части: одну, содержащую мнимые компоненты (i, j, k), и другую — реальную. Мнимая часть получила название «вектор». Векторы позволили описывать пространственные величины, такие как сила, скорость и положение, с указанием их направления и величины. В физике и инженерии это стало важнейшим инструментом для расчётов.

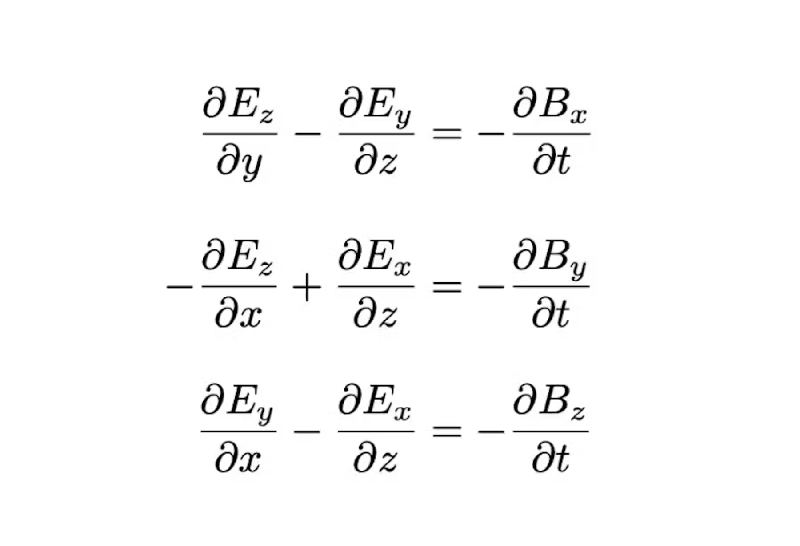
Позже, в конце XIX века, английский инженер Оливер Хевисайд упростил подход Гамильтона, заменив мнимые числа на реальные единичные векторы i, j, k. Это помогло сделать векторный анализ ещё более удобным и применимым в самых разных областях, включая электромагнетизм, механические расчёты и проектирование сложных систем. Векторное умножение, предложенное Гамильтоном, тоже получило широкое распространение: оно используется для расчёта силы, которая возникает в магнитных полях, при движении частиц и в других приложениях.

Гамильтон не дожил до того момента, когда его открытие обрело признание. Однако сегодня его наследие живёт в каждом программном продукте, каждом математическом расчёте, связанном с вращениями и движениями объектов. Кватернионы, которые когда-то выглядели как математическое любопытство, остаются одним из важнейших инструментов в таких областях, как астрономия, физика, компьютерная графика и навигация. Более того, ежегодно 16 октября энтузиасты математики совершают прогулку по маршруту Гамильтона, чтобы отметить его вклад в науку, который до сих пор влияет на современный мир.