Математики нашли доказательство 122-летней головоломки «Треугольник-квадрат»

Около десяти лет назад Тонан Камата , ныне работающий математиком в Японском институте передовых научных и технологических исследований (JAIST), оказался заворожён странной экспозицией в музее математики. Там демонстрировалась фигура, напоминающая оригами: треугольная плитка, разрезанная на четыре части и соединённая крошечными шарнирами. Одним движением её можно было повернуть так, чтобы из треугольника получился квадрат.

Этот экспонат уходит корнями к математической головоломке, впервые опубликованной в газете в 1902 году. Генри Дюдени , самоучка и автор головоломок, предложил читателям разрезать равносторонний треугольник на минимальное количество частей, чтобы из них можно было сложить квадрат. Через две недели он отметил, что некий «г-н С. У. Макэлрой из Манчестера» — клерк Чарльз Уильям Макэлрой, регулярно присылавший ему решения — нашёл четырёхчастный вариант. В следующем выпуске Дюдени сообщил, что никто из остальных читателей не смог найти лучший вариант. С тех пор рекорд держался, хотя и оставался недоказанным: возможно ли, что существует более оптимальное разбиение? Эта задача получила название «разрезание Дюдени» или «проблема галантерейщика» и даже была опубликована в выпуске Scientific American за июнь 1958 года . Известный математик Мартин Гарднер посвятил ей колонку. И вот, спустя 122 года после постановки задачи, Камата и двое других математиков доказали: четырёхчастное решение действительно оптимально. Их работа опубликована в препринте на arXiv под названием “ Dudeney’s Dissection Is Optimal ”.

«Думаю, многие любители математики согласятся: чем проще выглядит нерешённая задача, тем более она притягательна», — говорит Камата.

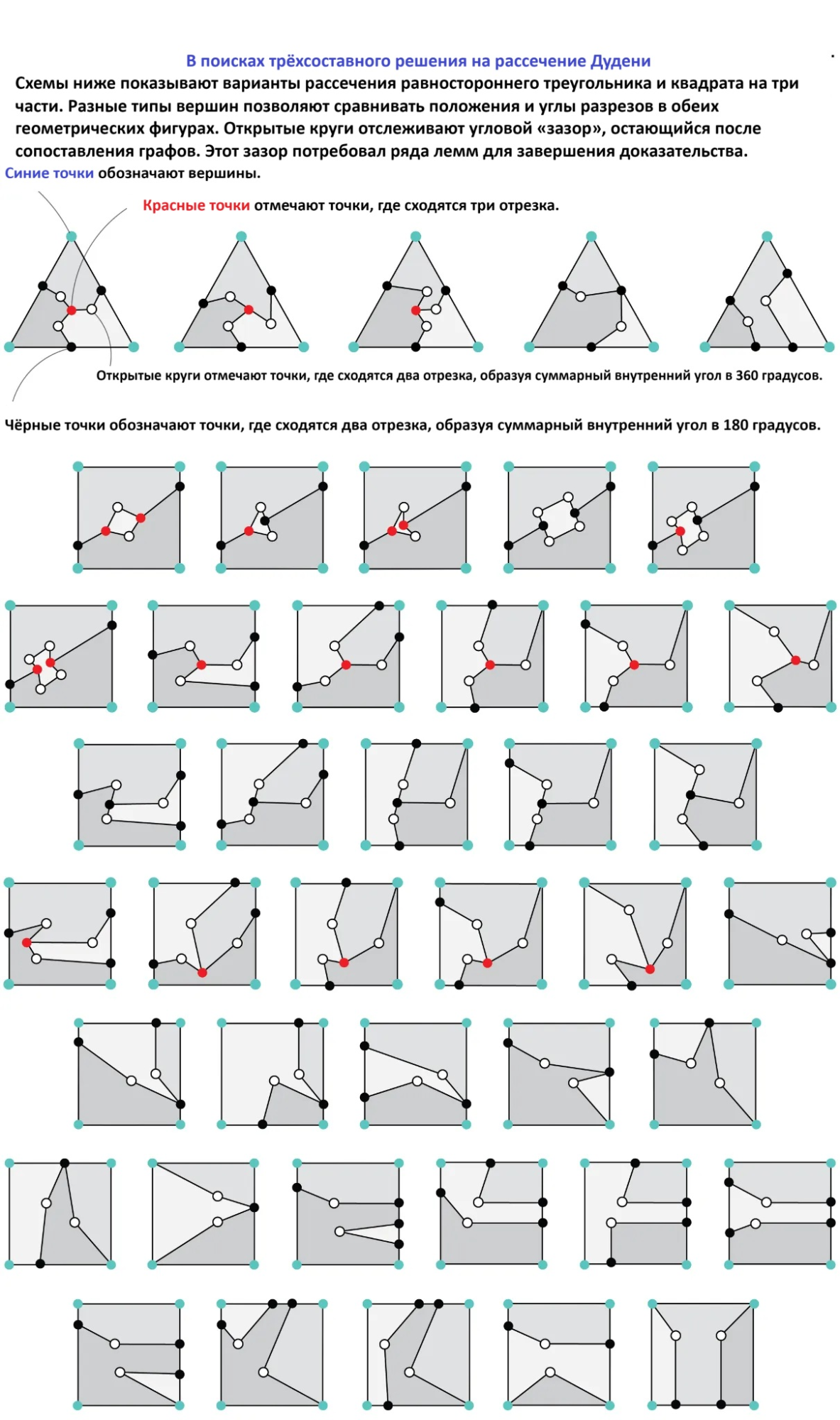
Совместно с математиком Массачусетского технологического института Эриком Демейном и коллегой из JAIST Рюхэем Уэхарой, Камата разрабатывал новый подход к задачам оригами через теорию графов. В этой области граф представляет собой совокупность рёбер и вершин, где можно сопоставлять структуры, выявляя глубинные закономерности. Именно этот путь учёные выбрали для изучения разрезания Дюдени.

Некоторые части доказательства оказались довольно простыми. Например, решение с двумя частями можно исключить, просто подумав об ограничениях задачи. Площадь фигуры должна оставаться одинаковой, а самый длинный возможный разрез квадрата — по диагонали — оказывается всё равно слишком коротким, чтобы соответствовать стороне равновеликого треугольника. Так двухчастное разбиение исключается сразу.

А вот с трёхчастными вариантами всё куда сложнее. Демейн поясняет: хотя кажется, что вариантов немного, на деле существует бесконечное количество способов разрезать треугольник на три части. У каждой части может быть сколь угодно много граней, а координаты разрезов могут начинаться в произвольных точках. «Здесь слишком много бесконечно возможных параметров. Просто перебором на компьютере такое не решить», — говорит он.

Чтобы обуздать хаос, команда классифицировала все возможные разрезания треугольника по способам, которыми линии пересекают его стороны. Всего они выделили пять уникальных классов. Затем проделали то же самое для квадрата и получили 38 классов.

Следующим шагом стало сопоставление: исследователи пытались найти такие пути в каждом классе, которые бы совпали между треугольником и квадратом. Это означало бы, что возможно трёхчастное разбиение.

Таким образом, непрерывная задача была частично сведена к дискретной. Но и внутри каждого класса по-прежнему оставалось бесконечно много возможных расположений вершин. В конечном счёте команда вывела набор сложных лемм — промежуточных шагов, которые с помощью доказательства от противного позволили исключить все совпадения.

Компьютерный учёный из колледжа Смит Джозеф О’Рурк, который много лет пытался решить эту головоломку и не участвовал в новом исследовании, считает, что доказательство ещё можно упростить. По его словам, авторам пришлось перебрать «множество запутанных и специфичных лемм», и большинство других исследователей, скорее всего, сдались бы на этом пути.

Если же авторам удастся сократить и обобщить своё доказательство, их метод сопоставления диаграмм может помочь решить и другие нерешённые задачи, связанные с оригами и трансформациями фигур. «Эти задачи напоминают нам, как много ещё предстоит открыть, — говорит Камата. — Каждый может стать первопроходцем на этом математическом фронтире».