Отвергните первые 37% вариантов: формула успешного выбора от математиков

Иногда жизнь превращается в череду мучительных выборов. Купить эту квартиру или ту? Снимать с этим соседом или с другим? Остаться с «почти идеальным» или ждать настоящего идеала? Порой кажется, что легче вообще ничего не решать. Но, как ни странно, у математики есть довольно изящный ответ на вопрос: как принимать такие решения с наибольшим шансом на успех?

Ещё в 1960 году математик и популяризатор науки Мартин Гарднер предложил логическую задачку , ставшую классикой: так называемую «проблему секретаря». Суть проста. Представим, что у вас есть n кандидатов на должность секретаря. Вы проводите собеседования по одному, в случайном порядке. Каждый кандидат может быть либо принят, либо отвергнут сразу же — вернуться к уже отвергнутому нельзя. Вам нужен лучший из всех, а не просто «достаточно хороший».

Та же логика применялась к «проблеме жениха» (ищем идеального партнёра) или к «игре в гугол» (ищем самое большое число на случайных карточках). Во всех случаях вопрос один: каковы шансы выбрать лучший вариант, если вы не знаете заранее, какой из них действительно лучший?

Математик Томас Фергюсон ещё в 1989 году предложил элегантное решение: сначала нужно сознательно отвергнуть первые r–1 вариантов (где r — любое целое число больше 1), просто чтобы составить представление об уровне предложений. А затем — выбрать первого кандидата, который окажется лучше всех, кого вы видели до этого момента. Главное — не брать никого из первой части потока, а просто наблюдать. И вот уже после этой стартовой фазы можно брать лучшего из оставшихся.

Теперь ключевой вопрос: в какой момент нужно остановить «отбор без выбора» и начать выбирать? Допустим, мы останавливаемся на m-м кандидате, отказываем всем до него и далее действуем по схеме. Если самый лучший оказался на позиции m+1 — вы в выигрыше. Но если он был на позиции m+2, возможны два сценария: либо вы уже выбрали предыдущего и пропустили лучшего, либо всё ещё ждёте — и тогда есть шанс поймать нужного. По расчетам, вероятность не промахнуться здесь — m / (m+1). Если лучший находится на позиции m+3, то шанс — m / (m+2). Общая формула — m / (n–1), если лучший кандидат — n-й.

Когда n стремится к бесконечности, эти выражения превращаются в предел. Вероятность успеха, которую Фергюсон обозначает как ϕ(r), становится интегралом. Максимизировать её можно, выбрав r, равное примерно n / e — то есть 1/e ≈ 0,368. Или, проще говоря: оптимально отвергнуть первые 37% вариантов и взять следующего, кто окажется лучше всех предыдущих. Шанс успеха — тоже около 37%.

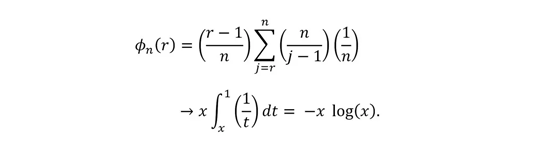
Пусть это звучит не слишком впечатляюще, но альтернатива гораздо хуже: если выбирать случайно, вы получите шанс всего 1/n — например, всего 5%, если у вас 20 потенциальных вариантов. А если следовать правилу 37%, вероятность получить лучшего увеличивается почти до 38,4%.

Конечно, метод не идеален. Представьте, что «тот самый» оказался как раз в первой трети — вы его отвергли и уже не вернётесь. Но если вы готовы немного смягчить критерии и искать не абсолютного победителя, а просто кого-то из верхнего процента, шансы растут. Например, если вы согласны на партнёра из лучших 5%, то достаточно отказаться от первых 22% и взять первого, кто покажется лучше всех до этого. Так можно достигнуть 57% вероятности удачного выбора. А если согласиться на кого-то из лучших 15%, можно и вовсе получить почти 80% шанс на успех.

Так что, возможно, секрет не в том, чтобы искать идеал, а в том, чтобы правильно расставлять приоритеты. В любви, в карьере, в выборе квартиры — везде может сработать та же формула: сначала отказываемся, наблюдаем, учимся отличать хорошее от посредственного. А потом — принимаем лучшее, что появится. Или, по крайней мере, лучшее из увиденного. И это уже неплохо.